Épreuve d’Informatique – Session 2024 – Filière MP
Remarques générales :
- Cette épreuve est composée d’un exercice et de deux parties tous indépendants.
- Toutes les instructions et les fonctions demandées seront écrites en Python.
- Les questions non traitées peuvent être admises pour aborder les questions ultérieures.
- Toute fonction peut être décomposée, si nécessaire, en plusieurs fonctions.
Important :
Le candidat doit impérativement commencer par traiter toutes les questions de l’exercice ci-dessous, et écrire les réponses dans les premières pages du cahier de réponses.
Exercice : (4 points)
L’exponentiation rapide est un algorithme de complexité logarithmique O(log n), qui permet de calculer $x^n$.
Fonction puiss (x, n) :
p <- 1
Tant que n ≠ 0 faire
Si n est impair Alors
p <- p*x
Fin Si
x <- x²
n <- n/2
Fin Tant que
Retourner pQ.1
Écrire la fonction puiss(x, n) qui reçoit en paramètres un réel x et un entier positif n. En utilisant l’algorithme de l’exponentiation rapide, la fonction retourne la valeur de $x^n$.
Un polynôme à coefficients réels est représenté par une liste L : chaque élément L[i] contient le coefficient du monôme de degré i.
Exemples :
- Le polynôme
7 + 4x – 3x² + x⁵est représenté par la liste[7, 4, -3, 0, 0, 1]. - La liste
[5, -2, 0, -4, 7, 0, -2]représente le polynôme– 2x⁶ + 7x⁴ – 4x³ – 2x + 5.
Q.2
Écrire la liste qui représente le polynôme – 3x³ + 7x² – x⁶ + 10 – 2x⁴.
Q.3
Écrire la fonction valeur(x, L) qui reçoit en paramètres un réel x et une liste L représentant un polynôme. En utilisant la fonction puiss, la fonction retourne l’image de x par le polynôme L.
Exemple :
valeur(3, [5, -2, 0, -4, 7, 0, -2]) # retourne -1000Q.4
Déterminer la complexité de la fonction valeur(x, L) avec justification.
Q.5
Écrire la fonction images(X, L) qui reçoit en paramètres une liste de réels X et une liste L représentant un polynôme. La fonction retourne la liste Y contenant les images des éléments de X par le polynôme L.
Q.6
On note le polynôme L² = L ∘ L (L rond L, 2 fois) et Lⁿ = L ∘ L ∘ … ∘ L (n fois). Écrire la fonction compose(x, L, n) qui reçoit en paramètres un réel x, une liste L représentant un polynôme, et un entier n > 0. La fonction retourne l’image de x par le polynôme composé Lⁿ.
Partie I : Programmation et Calcul Scientifique
Produit d’une chaîne matricielle
Dans cette partie, on suppose que le module numpy est importé :
import numpy as npLe produit matriciel d’une chaîne de matrices (séquence d’au moins deux matrices) est un problème d’optimisation qui permet de trouver le moyen le plus efficace pour calculer le produit de plusieurs matrices.
La multiplication matricielle est associative, ce qui signifie que, peu importe comment le produit est mis entre parenthèses, le résultat obtenu restera le même. Par exemple, pour quatre matrices $M_0$ de dimension $(20, 10)$ (20 lignes et 10 colonnes), $M_1$ de dimension $(10, 35)$, $M_2$ de dimension $(35, 8)$, et $M_3$ de dimension $(8, 12)$, on a :
$((M_0 \times M_1) \times M_2) \times M_3 = (M_0 \times (M_1 \times M_2)) \times M_3 = (M_0 \times M_1) \times (M_2 \times M_3) = M_0 \times ((M_1 \times M_2) \times M_3) = M_0 \times (M_1 \times (M_2 \times M_3))$
Cependant, l’ordre dans lequel le produit est mis entre parenthèses affecte le nombre de multiplications nécessaires pour calculer ce produit. Le nombre de multiplications dans chaque produit est présenté dans le tableau suivant :
| Produit matriciel | Compte des multiplications |
|---|---|
| $((M_0 \times M_1) \times M_2) \times M_3$ | $(20 \times 10 \times 35) + 20 \times 35 \times 8 + 20 \times 8 \times 12 = 14520$ |
| $(M_0 \times (M_1 \times M_2)) \times M_3$ | $10 \times 35 \times 8 + (20 \times 10 \times 8) + 20 \times 8 \times 12 = 6320$ |
| $(M_0 \times M_1) \times (M_2 \times M_3)$ | $(20 \times 10 \times 35) + (35 \times 8 \times 12) + 20 \times 35 \times 12 = 18760$ |
| $M_0 \times ((M_1 \times M_2) \times M_3)$ | $10 \times 35 \times 8 + ((10 \times 8 \times 12) + 20 \times 10 \times 12) = 6160$ |
| $M_0 \times (M_1 \times (M_2 \times M_3))$ | $35 \times 8 \times 12 + (10 \times 35 \times 12 + (20 \times 10 \times 12)) = 9960$ |
De toute évidence, le produit $M_0 \times ((M_1 \times M_2) \times M_3)$ est le plus efficace.
Énoncé du problème
On se donne une chaîne de $n$ matrices $M_0, M_1, M_2, \ldots, M_{n-1}$ (avec $n > 1$), et on souhaite calculer le produit matriciel : $M_0 \times M_1 \times M_2 \times \ldots \times M_{n-1}$ (on suppose que toutes les matrices ont des tailles compatibles, c’est-à-dire que le produit est bien défini). Le produit matriciel étant associatif, n’importe quel « parenthésage » du produit donnera le même résultat. Avant d’effectuer tout calcul, on cherche à déterminer quel « parenthésage » nécessitera le moins de multiplications.
Pour représenter la chaîne de matrices $M_0, M_1, \ldots, M_{n-1}$, on utilise une liste $T = [t_0, t_1, t_2, \ldots, t_n]$, telle que :
- $t_0$ est le nombre de lignes dans la matrice $M_0$
- $t_1$ est à la fois le nombre de colonnes dans $M_0$ et le nombre de lignes dans $M_1$
- $t_2$ est à la fois le nombre de colonnes dans $M_1$ et le nombre de lignes dans $M_2$
- …
- $t_{n-1}$ est à la fois le nombre de colonnes dans $M_{n-2}$ et le nombre de lignes dans $M_{n-1}$
- $t_n$ est le nombre de colonnes dans $M_{n-1}$
Exemple :
Soit $T = [20, 10, 35, 8, 12]$.
La liste $T$ représente la chaîne de matrices dont les tailles sont : $(20, 10), (10, 35), (35, 8)$ et $(8, 12)$.
A- Calcul du nombre minimum de multiplications dans le produit d’une chaîne matricielle
A.1 – Algorithme naïf
Une solution possible est de procéder par force brute en énumérant tous les « parenthésages » possibles pour en retenir le meilleur. L’idée est de décomposer le problème en un ensemble de sous-problèmes liés.
Pour calculer le nombre minimal de multiplications dans le produit matriciel de la chaîne de matrices $M_0, M_1, M_2, \ldots, M_{n-1}$ :
- On découpe cette séquence de matrices en deux séquences : $M_0, M_1, \ldots, M_k$ et $M_{k+1}, M_{k+2}, \ldots, M_{n-1}$ ;
- En utilisant la récursivité, on calcule $m1$ et $m2$ les deux nombres minimaux de multiplications dans le produit de chacune des deux séquences ;
- À la somme $m1 + m2$, on ajoute le nombre de multiplications dans le produit des deux matrices résultats des deux séquences ;
- Faire cela pour chaque position possible $k$ à laquelle la séquence de matrices peut être découpée, et prendre le minimum sur toutes.
Voici l’algorithme d’une fonction récursive qui calcule le nombre minimal de multiplications dans le produit d’une chaîne de matrices, représentée par la liste $T$. $i$ et $j$ sont deux indices dans la liste $T$ tels que $i < j$.
Fonction minProduit(T, i, j)
Si i = j - 1 Alors
Retourner 0
Fin Si
R ← liste vide
Pour k = i + 1 à j - 1 faire
c ← minProduit(T, i, k) + minProduit(T, k, j) + T[i] * T[k] * T[j]
Ajouter c à la liste R
Fin Pour
Retourner le minimum de R
Q.7
Écrire la fonction minProduit(T, i, j) qui reçoit en paramètres une liste T représentant une chaîne de matrices et deux indices $i$ et $j$ ($i < j$) dans $T$. La fonction retourne le nombre minimum de multiplications dans le produit de la chaîne de matrices représentée par la liste $T$.
Exemple:
T = [ 20, 10, 35, 8, 12 ]
minProduit (T, 0, len(T)-1) # retourne le nombre : 6160A.2 – Programmation dynamique Top-Down (Mémoïsation)
La fonction précédente minProduit n’est pas envisageable, sa complexité est exponentielle (elle fait appel à elle-même, plusieurs fois, avec les mêmes paramètres). Pour cela, on propose d’utiliser la mémoïsation :
On utilise un dictionnaire D, dans lequel on stocke les valeurs renvoyées par les appels de la fonction. Et lorsque la fonction est appelée à nouveau avec les mêmes paramètres, elle renvoie la valeur stockée dans le dictionnaire D, au lieu de la recalculer.
- Les clés du dictionnaire
Dsont les différents tuples d’indices $(i, j)$ tels que $0 \leq i < j < \text{taille de } T$ ; - La valeur de chaque clé $(i, j)$ de
Dest le nombre minimum de multiplications dans le produit de la chaîne de matrices représentée par la sous-liste $[T_i, T_{i+1}, \ldots, T_j]$.
Q.8
Écrire la fonction minPrd(T, i, j) qui reçoit en paramètres une liste T représentant une chaîne de matrices, i et j deux indices dans T tels que $i < j$. En utilisant le principe de la mémoïsation, la fonction retourne le nombre minimal de multiplications dans le produit de la chaîne de matrices représentée par T.
Exemple :
D = {}
T = [20, 10, 35, 8, 12]
minPrd(T, 0, len(T)-1) # retourne le nombre : 6160Le dictionnaire D contient les éléments suivants :
{ (0, 1): 0 , (1, 2): 0 , (2, 3): 0 , (3, 4): 0 , (2, 4): 3360 , (1, 3): 2800 , (1, 4): 3760 , (0, 2): 7000 , (0, 3): 4400, (0, 4): 6160 }A.3 – Programmation dynamique Bottom-Up
Le problème a une structure telle qu’un « sous-parenthésage » optimal est lui-même optimal. De plus, un même « sous-parenthésage » peut intervenir dans plusieurs « parenthésages » différents. Ces deux conditions rendent possible la mise en œuvre de la programmation dynamique.
On remarque que pour un parenthésage optimal du produit $M_i \times M_{i+1} \times \ldots \times M_j$, si le dernier produit matriciel calculé est $(M_i \times M_{i+1} \times \ldots \times M_k) \times (M_{k+1} \times M_{k+2} \times \ldots \times M_j)$, alors les « parenthésages » utilisés pour le calcul des produits $M_i \times M_{i+1} \times \ldots \times M_k$ et $(M_{k+1} \times M_{k+2} \times \ldots \times M_j)$ sont eux aussi optimaux.
La même hypothèse d’optimalité peut être faite pour tous les « parenthésages » de tous les produits intermédiaires au calcul du produit $M_i \times M_{i+1} \times \ldots \times M_j$ et donc tous ceux du calcul du produit $M_0 \times M_1 \times M_2 \times \ldots \times M_{n-1}$. Cela permet une résolution grâce à la programmation dynamique.
Pour calculer le nombre minimal de multiplication des « sous-parenthésages », on utilise une matrice carrée C de n lignes et n colonnes (n étant le nombre de matrices dans le produit), telle que chaque élément $C_{i,j}$ contient le nombre minimal de multiplications dans le produit matriciel $M_i \times M_{i+1} \times \ldots \times M_j$.
Pour calculer les éléments de la matrice C, on utilise l’algorithme (1) suivant :
Exemple :
$T = [20, 10, 35, 8, 12]$
La matrice $C$ contient les éléments suivants :
$$ \begin{bmatrix} 0 & 7000 & 4400 & 6160 \\ 0 & 0 & 2800 & 3760 \\ 0 & 0 & 0 & 3360 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$NB : L’élément en haut à droite de la matrice $C$ contient le nombre minimal de multiplications.
Les éléments de $C$ doivent être calculés de proche en proche, dans l’ordre des diagonales suivant :
| n-ème diagonale | Matrice C |
|---|---|
| Première diagonale | 7000 → 2800 → 3360 |
| Deuxième diagonale | 4400 → 3760 |
| Troisième diagonale | 6160 |
Q.9
Écrire la fonction matriceC(T) qui reçoit en paramètre une liste T représentant une chaîne de matrices. En utilisant l’algorithme (1) décrit précédemment, la fonction retourne la matrice C.
B – Recherche du « parenthésage » optimal
Pour trouver le « parenthésage » optimal qui correspond au nombre minimal de multiplications dans le produit de la chaîne de matrices, on utilise une matrice carrée P de même dimension que C, telle que chaque élément $P_{i,j}$ contient l’indice $k$ tel que le « parenthésage » optimal du produit soit $(M_i \times M_{i+1} \times \ldots \times M_k) \times (M_{k+1} \times M_{k+2} \times \ldots \times M_j)$.
Pour calculer les éléments de la matrice P, on utilise l’algorithme (2) suivant :
Exemple :
$T = [20, 10, 35, 8, 12]$
Les matrices C et P sont les suivantes :
Matrice C
$$ \begin{bmatrix} 0 & 7000 & 4400 & 6160 \\ 0 & 0 & 2800 & 3760 \\ 0 & 0 & 0 & 3360 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$Matrice P
$$ \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$Les éléments de P doivent être calculés de proche en proche, dans l’ordre des diagonales suivant :
| Matrice C | Matrice P | |
|---|---|---|
| Première diagonale | 7000 → 2800 → 3360 | 0 → 1 → 2 |
| Deuxième diagonale | 4400 → 3760 | 0 → 2 |
| Troisième diagonale | 6160 | 0 |
Q.10
Écrire la fonction matriceP(T, C) qui reçoit en paramètres une liste T représentant la chaîne de matrices et la matrice C. La fonction retourne la matrice P indiquant le meilleur parenthésage pour minimiser les multiplications.
C – Calcul du produit matriciel d’une chaîne de matrices
Chaque élément $P_{i,j}$ de la matrice $P$ contient l’indice $k$ tel que le « parenthésage » optimal du produit matriciel $M_i \times M_{i+1} \times \ldots \times M_k \times M_{k+1} \times \ldots \times M_j$ soit $(M_i \times M_{i+1} \times \ldots \times M_k) \times (M_{k+1} \times M_{k+2} \times \ldots \times M_j)$. Donc on peut utiliser les éléments de la matrice $P$ pour calculer le produit d’une chaîne matricielle.
Exemple :
On suppose que la liste $M$ contient les matrices d’une chaîne matricielle :
$M = [M_0, M_1, M_2, M_3]$
Et la matrice $P$ est la suivante :
$$ P = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$
À partir de la matrice $P$, on peut déduire que :
- Le « parenthésage » optimal du produit $M_0 \times M_1 \times M_2 \times M_3$ est $M_0 \times ((M_1 \times M_2) \times M_3)$ car $P_{0,3}$ vaut 0.
- Le « parenthésage » optimal du produit $M_1 \times M_2 \times M_3$ est $(M_1 \times M_2) \times M_3$ car $P_{1,3}$ vaut 2.
Ainsi, pour calculer le produit matriciel de la chaîne matricielle $M$, on peut utiliser la relation de récurrence suivante :
Soient $i$ et $j$ deux indices dans $M$ tels que $i \leq j$ :
- si $i = j$, alors $\text{produit}(M, i, i) = M_i$
- si $j = i + 1$, alors $\text{produit}(M, i, j) = M_i \times M_j$
- si $j > i + 1$, alors $\text{produit}(M, i, j) = \text{produit}(M, i, P_{i,j}) \times \text{produit}(M, P_{i,j} + 1, j)$
Rappel : Le module numpy contient la méthode dot, qui permet de calculer le produit matriciel de deux matrices.
Q.11 – Écrire la fonction produit_matriciel(M) qui reçoit en paramètre la liste $M$ contenant au moins deux matrices compatibles pour le produit matriciel. La fonction calcule le produit matriciel des matrices de $M$, en utilisant le « parenthésage » optimal, et elle retourne la matrice résultante.
Exemple :
$M = [M_0, M_1, M_2, M_3]$.
La fonction produit_matriciel(M) retourne la matrice résultat du produit matriciel de la chaîne de matrices $M$, en utilisant le « parenthésage » optimal : $M_0 \times ((M_1 \times M_2) \times M_3)$.
Partie II : Problème – Segmentation d’image
Une image matricielle est représentée par une matrice. Chaque élément de la matrice est appelé : pixel. Il existe plusieurs modes pour représenter les couleurs des pixels. Le plus utilisé est l’espace colorimétrique RVB pour Rouge, Vert, Bleu (ou RGB – Red, Green, Blue).
Cet espace est basé sur une synthèse additive des couleurs. Il consiste essentiellement à représenter une couleur par trois nombres entiers compris entre 0 et 255, qui représentent les intensités respectives du rouge, du vert et du bleu. Le mélange des trois composantes à leur valeur maximum donne du blanc, à l’instar de la lumière. Le nombre de couleurs différentes pouvant être ainsi représenté est de $256^3$ possibilités, soit environ 16,7 millions de couleurs.
Comme la différence de nuance entre deux couleurs très proches, mais différentes dans ce mode de représentation, est quasiment imperceptible pour l’œil humain, on considère commodément que ce système permet une restitution exacte des couleurs, c’est pourquoi on parle de couleurs vraies.
Exemple:

Cette image est représentée par la matrice $M$, de dimension : 730 lignes et 950 colonnes :
$$ \begin{bmatrix} [148, 155, 148], & [143, 150, 143], & [143, 150, 143], & \ldots, & [153, 161, 163] \\ [145, 152, 145], & [143, 150, 143], & [142, 149, 142], & \ldots, & [151, 159, 161] \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ [31, 35, 18], & [48, 52, 35], & [54, 58, 44], & \ldots, & [43, 75, 10] \\ \end{bmatrix} $$
Par exemple, la liste $[148, 155, 148]$ est l’élément $M_{0,0}$. Cette liste représente la couleur du pixel d’indices $(0,0)$ dans l’image représentée par la matrice $M$.
NB : Dans la suite de cette partie, on utilisera la matrice $M$ dans les exemples des fonctions.
Q.12
Quel est le nombre minimal de bits nécessaire pour coder un entier sans signe, compris entre 0 et 255 ?
Q.13
Donner la taille en Kilo Octet (Ko) d’une image couleur représentée par une matrice de 1000 lignes et 1800 colonnes.
Histogramme d’une image couleur
Q.14 – Écrire la fonction histogramme(M) qui reçoit en paramètre une matrice $M$ représentant une image couleur. La fonction retourne une matrice $H$ qui représente l’histogramme de l’image, telle que :
- La dimension de la matrice $H$ est : 3 lignes, 256 colonnes ;
- La valeur de chaque élément $H_{0,i}$ est le compte des pixels de $M$, ayant la valeur $i$ pour l’intensité du rouge ;
- La valeur de chaque élément $H_{1,i}$ est le compte des pixels de $M$, ayant la valeur $i$ pour l’intensité du vert ;
- La valeur de chaque élément $H_{2,i}$ est le compte des pixels de $M$, ayant la valeur $i$ pour l’intensité du bleu.
Exemple :
La fonction histogramme(M) retourne la matrice $H$ suivante :
$$ H = \begin{bmatrix} [7, 5, 14, 11, \ldots, 59, 18, 15, 14, 12, 32, 29, 37, 41, 47, 36, 40, 47, 67, 53, 67, 67, 70, 56, \ldots, 84, 153], \\ [6, 2, 5, 4, 10, 7, 8, 14, 14, 19, 24, 24, 25, 29, 23, 24, 34, 32, 47, 40, 42, 44, 46, 51, 53, \ldots, 98, 153], \\ [117, 54, 76, 85, 94, 97, 99, 112, 113, 99, 101, 111, 119, 119, 103, 105, 101, 110, 123, \ldots, 477, 2742] \end{bmatrix} $$
Q.15 – Écrire la fonction representation(H) qui reçoit en paramètre la matrice $H$ représentant l’histogramme d’une image couleur, et qui trace les trois courbes (Rouge, Vert, Bleu) représentatives de l’histogramme.
On suppose que le module matplotlib.pyplot est importé :
import matplotlib.pyplot as pltExemple:
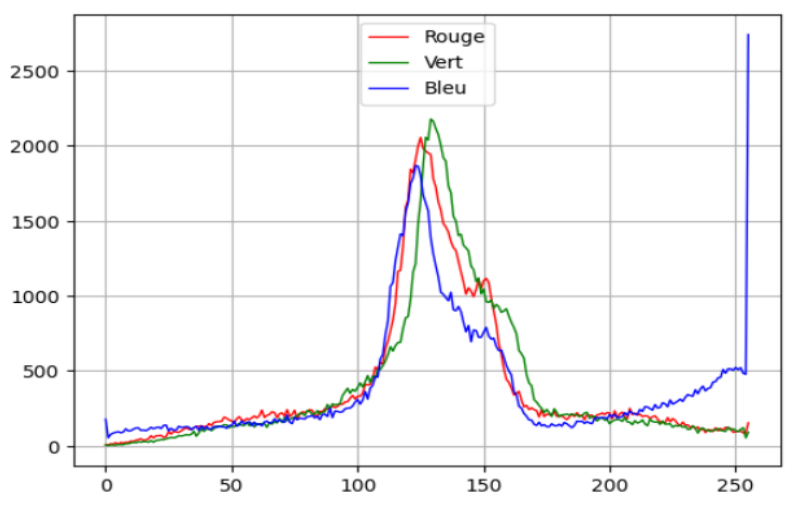
Segmentation d’image avec K-means
Segmentation d’une image, c’est quoi ?
La segmentation d’une image est une technique qui consiste à découper de façon automatique une image en zones de pixels appartenant à une même classe d’objets. La segmentation d’images a de nombreuses applications, notamment en imagerie médicale, analyse d’images satellitaires, voitures autonomes, etc.
La segmentation d’une image est à la base un problème de classification de pixels. Chaque pixel de l’image doit être associé à un ensemble d’autres pixels, que l’on affecte à une classe. L’objectif de la segmentation d’une image est de changer sa représentation en quelque chose de plus significatif et plus facile à analyser.
Une des méthodes envisageables pour séparer les pixels en classes est l’utilisation de l’algorithme K-means.
L’algorithme K-means (K-moyennes) est l’un des algorithmes de clustering (algorithmes non supervisés) utilisés dans la segmentation d’une image en plusieurs clusters : Les pixels de l’image ayant des couleurs similaires sont regroupés dans le même cluster.
Pour la segmentation d’une image $M$, le principe de l’algorithme K-means est le suivant :
- Définir la fonction qui calcule la distance entre deux pixels ;
- Choisir un entier $k$ non nul, qui représente le nombre de clusters (groupes) ;
- Choisir une liste de $k$ pixels différents dans $M$. Ces pixels sont appelés centroïdes ;
- Construire $k$ clusters : Chaque cluster contient les pixels de $M$ qui possèdent le même plus proche centroïde ;
- Mettre à jour la liste des centroïdes : Calculer le nouveau centroïde de chaque cluster ;
- Répéter les étapes 4 et 5 jusqu’à convergence : la convergence correspond au fait que les centroïdes ne changent pas après une mise à jour. Mais cette convergence n’est pas garantie. Il faut donc arrêter après un nombre maximal de $n$ répétitions.
Distance entre deux pixels
Pour la mesure de similarité entre deux pixels, on propose d’utiliser la distance de Manhattan.
$X$ et $Y$ étant deux listes contenant les couleurs de deux pixels. La distance de Manhattan entre ces deux pixels est définie comme la somme des valeurs absolues des différences de chacun de leurs attributs. Elle est exprimée par la formule suivante :
$$ \text{distance}(X, Y) = \sum_{i=0}^{2} |X_i – Y_i| $$
Q.16 – Écrire la fonction distance(X, Y) qui reçoit en paramètres deux listes $X$ et $Y$ représentant les couleurs de deux pixels. La fonction retourne la valeur de la distance de Manhattan entre les deux pixels $X$ et $Y$.
Exemple :
distance([239, 230, 247], [127, 132, 125]) retourne le nombre 332
Initialisation des centroïdes
Rappel : On suppose que la méthode randint du module random est importée.
La méthode randint reçoit en paramètres deux entiers $a$ et $b$ ($a \leq b$), et elle renvoie un entier $x$ choisi aléatoirement entre $a$ et $b$.
Exemple : random(0, 100) renvoie 63
Q.17
Écrire la fonction init_centroides(M, k) qui reçoit en paramètres la matrice M qui représente une image couleur, et k un entier strictement positif. La fonction retourne une liste C contenant k différents pixels choisis de façon aléatoire dans la matrice M.
Exemple :
init_centroides (M, 3) retourne la liste C = [ [ 150, 160, 152 ], [ 119, 124, 118 ], [ 187, 177, 250 ] ]
Plus proche centroïde
Q.18
Écrire la fonctionproche_centroide(P, C) qui reçoit en paramètres une liste $P$ qui représente un pixel, et la liste $C$ des centroïdes. La fonction retourne l’indice du centroïde de $C$ le plus proche au pixel $P$, selon la distance de Manhattan.
Exemples :
$C = [ [150, 160, 152], [119, 124, 118], [187, 177, 250] ]$
proche_centroide([137, 140, 133], C)retourne 1 [$119, 124, 118$ est le plus proche à ce pixel]proche_centroide([207, 205, 255], C)retourne 2 [$187, 177, 250$ est le plus proche à ce pixel]proche_centroide([154, 130, 170], C)retourne 0 [$150, 160, 152$ est le plus proche à ce pixel]
Segmentation de l’image
La liste $C$ contient $k$ centroïdes. La segmentation de l’image consiste à créer une nouvelle matrice $R$ de même dimension que $M$. La valeur de chaque élément $R_{i,j}$ est l’indice du centroïde de $C$ le plus proche au pixel $M_{i,j}$.
Q.19
Écrire la fonctionsegmentation(M, C) qui reçoit en paramètres la matrice $M$ qui représente une image couleur, et la liste $C$ des centroïdes. La fonction retourne la matrice $R$.
Exemple :
$C = [ [150, 160, 152], [119, 124, 118], [187, 177, 250] ]$
segmentation(M, C) retourne la matrice $R$ suivante :
$$ R = \begin{bmatrix} 0 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 2 & 2 & 2 & 2 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{bmatrix} $$
Q.20
Mise à jour de la liste des centroïdes
Un centroïde est la moyenne arithmétique de tous les pixels appartenant à un cluster particulier. Ainsi, pour calculer le nouveau centroïde $c$ d’un cluster de $n$ pixels, on utilise la formule suivante, qui permet de calculer chaque composante $c_q$ ($q=0$ pour le rouge, $q=1$ pour le vert, ou $q=2$ pour le bleu) :
$$ c_q = \frac{1}{n} \sum M_{i,j,q} \quad \text{pour tout pixel } M_{i,j} \text{ du même cluster} $$
Q.20 – Écrire la fonction nv_centroide(M, R, g) qui reçoit en paramètres la matrice $M$ qui représente une image couleur, la matrice $R$ des indices des centroïdes et $g$ un entier positif qui représente l’indice d’un centroïde ($g$ est un élément de $R$). La fonction retourne une nouvelle liste qui représente le nouveau centroïde de tous les pixels de $M$ tels que $g$ est l’indice du centroïde le plus proche à ces pixels.
Exemples :
nv_centroide(M, R, 0)retourne le centroïde $[149, 152, 152]$nv_centroide(M, R, 1)retourne le centroïde $[108, 114, 113]$nv_centroide(M, R, 2)retourne le centroïde $[198, 192, 239]$
Épreuve d’Informatique – Session 2024 – Filière MP
Q.21
Écrire la fonctionmaj_centroides(M, R, k) qui reçoit en paramètre la matrice $M$ qui représente une image couleur, la matrice $R$ des indices des centroïdes et $k$ un entier strictement positif qui représente le nombre de clusters. La fonction retourne une nouvelle liste $C$ qui contient les nouveaux centroïdes de chaque cluster.
Exemple :
maj_centroides(M, R, 3) retourne la nouvelle liste $C$ contenant trois centroïdes :
$C = [ [149, 152, 152], [108, 114, 113], [198, 192, 239] ]$
Q.22
Écrire la fonctionkmeans(M, k, n) qui reçoit en paramètres la matrice $M$ qui représente une image couleur, $k$ un entier strictement positif qui représente le nombre de clusters et $n$ un entier strictement positif qui représente le nombre maximal de répétitions. En utilisant l’algorithme k-means, la fonction effectue la segmentation de l’image $M$ en $k$ clusters, et elle retourne la matrice $R$ des indices des centroïdes et la liste $C$ des centroïdes des clusters de $R$.
Recherche du nombre k optimum (méthode Elbow)
Pour un même jeu de données, il y a de nombreux partitionnements possibles. Il faut donc choisir le nombre de clusters $k$ le plus pertinent pour mettre en lumière les patterns intéressants.
Hélas, il n’existe pas de procédé automatique pour cela. Parmi les méthodes pour déterminer le nombre $k$ idéal, il existe la méthode Elbow (méthode du coude).
La méthode Elbow s’appuie sur la notion d’inertie intraclasse. On définit cette dernière comme ceci : la somme des distances entre chaque pixel et son centroïde associé, puis à placer les inerties obtenues sur un graphique. On obtient alors une visualisation en forme de coude, sur laquelle le nombre optimal de clusters est le point représentant la pointe du coude, c’est-à-dire celui correspondant au nombre de clusters à partir duquel la variance ne baisse plus significativement.
Exemple :
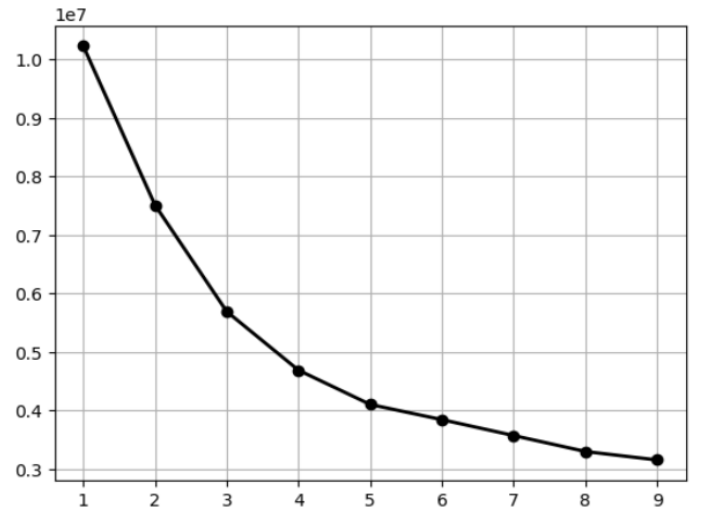
Q.23
Écrire la fonctioncalcul_inertie(M, R, C) qui reçoit en paramètres la matrice $M$ qui représente une image couleur, la matrice $R$ des indices des centroïdes et la liste $C$ des centroïdes. La fonction retourne la somme des distances entre chaque pixel et son centroïde associé (centroïde le plus proche à chaque pixel).
Exemple :
calcul_inertie(M, R, C) retourne le nombre 5694464
Q.24
Écrire la fonctioninerties(M, n) qui reçoit en paramètres la matrice $M$ qui représente une image couleur et $n$ un entier strictement positif qui représente le nombre maximal de répétitions. La fonction retourne un dictionnaire des inerties tel que :
- Les clés du dictionnaire sont les valeurs de $k$, pour $k=1, 2, 3, 4, \ldots, 9$ ;
- La valeur de chaque clé est l’inertie correspondante à chaque valeur de $k$.
Exemple :
inerties(M, 50) #retourne le dictionnaire des inerties suivant :
# {1 : 10231898, 2 : 7520058, 3 : 5694464, 4 : 4790619, 5 : 4126946, 6 : 3895363, 7 : 3396162, 8 : 3099661, 9 : 3053467}Base de données et SQL
Base de données et langage SQL
Après la segmentation de l’image en plusieurs clusters, on propose de représenter l’image segmentée par une base de données composée d’une seule table : Segmentation.
Segmentation
ligne (Entier)
colonne (Entier)
rouge (Entier)
vert (Entier)
bleu (Entier)
cluster (Entier)
La table Segmentation est composée des champs suivants :
- Le champ ligne contient un entier qui représente l’indice de la ligne du pixel ;
- Le champ colonne contient un entier qui représente l’indice de la colonne du pixel ;
- Le champ rouge contient un entier qui représente l’intensité du rouge du pixel ;
- Le champ vert contient un entier qui représente l’intensité du vert du pixel ;
- Le champ bleu contient un entier qui représente l’intensité du bleu du pixel ;
- Le champ cluster contient un entier qui représente le cluster auquel appartient le pixel.
Exemples :
| ligne | colonne | rouge | vert | bleu | cluster |
|---|---|---|---|---|---|
| 0 | 67 | 78 | 120 | 57 | 0 |
| 0 | 68 | 62 | 106 | 43 | 0 |
| 2 | 66 | 91 | 125 | 75 | 1 |
| 3 | 40 | 165 | 171 | 171 | 1 |
| 4 | 47 | 198 | 193 | 223 | 1 |
| 0 | 0 | 148 | 155 | 148 | 2 |
| … | … | … | … | … | … |
Q.25 – Déterminer la clé primaire de la table Segmentation. Justifier votre réponse.
Q.26 – Écrire, en algèbre relationnelle, une requête qui donne pour résultat les lignes, les colonnes, les intensités du rouge, du vert et du bleu des pixels du cluster 0 et des pixels du cluster 2.
Q.27 – Écrire une requête SQL qui donne pour résultat les lignes, les colonnes, les intensités du rouge, du vert et du bleu des pixels du cluster 1 et des pixels du cluster 2, triés dans l’ordre croissant des lignes et colonnes.
Q.28 – Écrire une requête SQL qui donne pour résultat les différents clusters, le compte de pixels dans chaque cluster, l’intensité du rouge du centroïde de chaque cluster, triés dans l’ordre décroissant des comptes des pixels. L’intensité du rouge du centroïde doit être comprise entre 100 et 200.
Q.29 – Écrire une requête SQL qui donne pour résultat la moyenne des comptes de pixels par cluster.
**************** FIN ****************
