Exercice : L’algorithme RLE pour la compression de chaînes de caractères
La compression de données est le traitement informatique utilisant un algorithme particulier, qui permet de transformer une suite de bits A en une suite de bits B plus courte. Les suites A et B contiennent les mêmes informations, mais codées de manière différente.
L’algorithme RLE (Run-Length Encoding), appelé en français codage par plages, est un algorithme de compression informatique qui consiste à repérer et à éliminer la redondance des données. Toute suite de caractères identiques est remplacée par un couple (caractère répété suivi de son nombre d’occurrences).
Exemples :
- s1= »CCCCBBBRC » donne : s2= »C4B3R1C2″
- s1= »AAARTTAAVVTTTT », sa chaîne compressée donne : s2= »A3R1T2A2V2T3″
Question :
Écrire la fonction compresser(ch) qui prend en paramètre une chaîne de caractères ch et qui retourne la compression de ch selon l’algorithme RLE.
Problème : Codage cyclique
On se propose d’implanter plusieurs techniques de détection d’erreurs dans la transmission de données sur des moyens de communication non fiables. Les données transitant sur le réseau sont des séquences de bits que l’on notera 0 et 1. Ces séquences de bits sont découpées en mots b0, b1, ..., bn-1 de longueur n (n > 0).
Ces mots sont représentés par des tableaux d’entiers b de longueur n dont l’élément bi à l’indice i vaut 0 ou 1 (0 <= i < n). Le nombre d’erreurs de transmission du mot b est le nombre de bits ayant changé de valeur après la transmission.
Exemple :
Le mot b = [1,1,0,1,1,0,0] de taille n=7 sera représenté en Python par la liste suivante :
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| b | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Partie I : Bit de parité
Le ou-exclusif x ⊕ y de deux bits x et y est défini par la table des valeurs suivante :
| x | y | x ⊕ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
On remarque qu’on a : 0 ⊕ x = x et x ⊕ x = 0 pour toute valeur de x. Donc x est son propre opposé pour ⊕.
Question 1 :
✎ Écrire la fonction ou_exclusif(x, y) qui calcule et retourne le ou-exclusif $x \oplus y$ des deux bits $x$ et $y$ pris comme arguments.
Exemple :
L’appel de la fonction ou_exclusif(1, 0) retourne 1.
La technique du bit de parité consiste à ajouter un bit $b_n$ (le bit de parité) aux données utiles $[b_0, b_1, \ldots, b_{n-1}, b_n]$ de façon à ce que $[b_0, b_1, \ldots, b_n]$ ait un nombre pair de bits à 1.
Ainsi, pour le tableau [1, 1, 0, 1, 1, 1, 0] on a 7 bits et 5 uns, donc le bit de parité sera 1. Le mot transmis sur le réseau est [1, 1, 0, 1, 1, 1, 0, 1]. Schématiquement, on aura :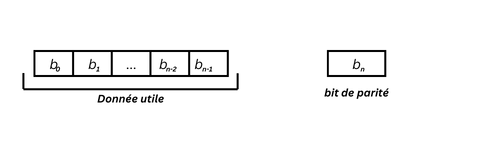
Question 2 :
✎ Écrire la fonction nombre1(b) qui prend en paramètre un mot $b$ et qui calcule et retourne le nombre de bits égaux à 1 dans $b$.
Exemple :
L’appel de la fonction nombre1([1, 1, 0, 1, 1, 1, 0]) retourne 5.
Question 3 :
✎ Écrire la fonction bit_parite(b) qui prend en paramètre un mot bbb et qui retourne un mot (avec bit de parité) qui sera transmis sur le réseau.
Exemple :
L’appel de la fonction bit_parite([1, 1, 0, 1, 1, 1, 0]) retourne le mot :[1, 1, 0, 1, 1, 1, 0, 1]
Question 4 :
✎ Écrire la fonction erreurs(b1, b2) qui prend en paramètre le mot b1 avant la transmission et le mot b2 après la transmission, et qui retourne le nombre d’erreurs de transmission.
Exemple :
L’appel de la fonction erreurs([1, 1, 0, 1, 1, 1, 0], [1, 0, 1, 1, 0, 1, 0]) retourne 3.
Partie II : Codage CRC
On peut considérer le tableau $b$ de $n$ bits $[b_0, b_1, \ldots, b_{n-1}]$ comme les coefficients du polynôme :$P(X) = b_0 X^{n-1} + b_1 X^{n-2} + \ldots + b_{n-2} X + b_{n-1}$
Le degré du polynôme $P(X)$ est la valeur maximale de $k$ telle que $b_{n-1-k}$ ne soit pas nul.
Question 5 :
✎ Écrire la fonction degre(b) prenant en argument un tableau b de coefficients représentant le polynôme $P(X)$, et retournant le degré de $P$ (par convention, le degré du polynôme nul vaudra -1).
Exemple :
Soit le mot suivant :
$$\begin{array}{c|c|c|c|c|c|c} i & 0 & 1 & 2 & 3 & n-3 & n-2 & n-1 \\ \hline b & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ \end{array}$$
L’appel de la fonction degre(b) retourne 4.
La somme exclusive des deux polynômes $P(X)$ et $Q(X)$, dont les coefficients sont les tableaux $[b_0, b_1, \ldots, b_{n-1}]$ et $[C_0, C_1, \ldots, C_{n-1}]$, est définie par :$$P(X) \oplus Q(X) = (b_0 \oplus C_0) X^{n-1} + (b_1 \oplus C_1) X^{n-2} + \ldots + (b_{n-2} \oplus C_{n-2}) X + (b_{n-1} \oplus C_{n-1})$$
Remarque :
$P(X)$ est son propre opposé, puisque $P(X) \oplus P(X) = 0$.
Question 6 :
✎ Écrire la fonction plus(b, C) prenant comme arguments deux tableaux $b$ et $C$ représentant deux polynômes $P(X)$ et $Q(X)$ et qui retourne un tableau $d$ représentant le polynôme somme.
Exemple :
L’appel de la fonction plus([1, 0, 1, 0, 0, 0, 0], [1, 0, 1, 0, 1, 1, 1]) retourne le polynôme de coefficients [0, 0, 0, 0, 1, 1, 1].
La technique, dite CRC (Cyclic Redundancy Check), ajoute plus de bits de contrôle à chaque mot transmis que la méthode du bit de parité. Elle considère un polynôme générateur $G(X)$, bien choisi, de degré $k$ ($0 < k \leq n$), une fois pour toutes ; et elle construit pour tout mot bbb, correspondant au polynôme $P(X)$, le reste $R(X)$ de la division euclidienne de $P(X) * X^k$ par $G(X)$.
$$R(X) = P(X) * X^k \mod G(X)$$
où mod est l’opération modulo.
Si $[r_0, r_1, \ldots, r_{k-1}]$ sont les coefficients de $R(X)$, la donnée transmise $[b_0, b_1, \ldots, b_{n-1}, r_0, r_1, \ldots, r_{k-1}]$ correspondra à un polynôme multiple de $G(X)$.
Graphiquement, on a :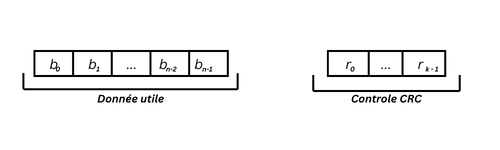
Pour calculer le reste $R(X)$ de la division de $P(X) * X^k$ par $G(X)$, on utilise l’algorithme classique de la division :
- On aligne les bits valant 1 les plus à gauche du dividende et du diviseur, puis on retranche le diviseur au dividende (grâce à l’opération $\oplus$).
- Le degré du résultat est strictement inférieur à celui du dividende.
- Et on recommence la division en prenant le résultat comme nouveau dividende, jusqu’à ce que son degré soit strictement inférieur à $k$.
Ainsi, par exemple, pour les tableaux $b = [0, 1, 1, 0, 1, 0, 0, 1]$ et $g = [0, 1, 0, 1]$ (et donc $k = 2$), les étapes successives de la division donnent :
Étape 1 :
On calcule $P(X) * X^2$qui donne : [0, 1, 1, 1, 0, 1, 0, 0].
Étape 2 :
On retranche le diviseur au dividende, ce qui donne [0, 0, 1, 0, 0, 1, 0, 0] : 
Étape 3 :
On recommence la division jusqu’à obtenir un reste strictement inférieur à $k$.
[0, 0, 0, 1, 1, 0, 0]
[0, 0, 0, 0, 1, 1, 0]
[0, 0, 0, 0, 0, 1, 1]
D’où la valeur [1, 1] pour le CRC.
Question 7 :
✎ Écrire la fonction CRC(b, g) prenant comme arguments deux tableaux $b$ et $g$, qui retourne le tableau des bits correspondant aux coefficients du CRC pour le mot $b$ en fonction du polynôme générateur $g$.
!! Le tableau $b$ ne doit pas être modifié.
Correction
Exercice
def compresser(ch):
if len(ch) == 0:
return ""
# Initialisation de la chaîne compressée et des compteurs
resultat = ""
compteur = 1
caractere_prec = ch[0]
# Boucle à travers chaque caractère de la chaîne
for i in range(1, len(ch)):
if ch[i] == caractere_prec:
# Si le caractère est identique au précédent, on incrémente le compteur
compteur += 1
else:
# Si le caractère est différent, on ajoute le caractère et son nombre d'occurrences
resultat += caractere_prec + str(compteur)
# Réinitialisation du compteur et du caractère précédent
caractere_prec = ch[i]
compteur = 1
# Ajouter le dernier caractère et son compteur
resultat += caractere_prec + str(compteur)
return resultat
# Exemples
s1 = "CCCCBBBRC"
s2 = "AAARTTAAVVTTTT"
print(compresser(s1)) # Retourne "C4B3R1C2"
print(compresser(s2)) # Retourne "A3R1T2A2V2T3"
Problème
Question 1.
def ou_exclusif(x, y):
if (x == 0 and y == 0) or (x == 1 and y == 1):
return 0
else:
return 1
Question 2.
def nombre1(b):
compteur = 0
for bit in b:
if bit == 1:
compteur += 1
return compteur
Question 3.
def bit_parite(b):
nombre_uns = nombre1(b)
if nombre_uns % 2 == 0:
b.append(0) # Ajoute 0 si le nombre de uns est pair
else:
b.append(1) # Ajoute 1 si le nombre de uns est impair
return b
Question 4.
def erreurs(b1, b2):
erreurs_count = 0
for i in range(len(b1)):
if b1[i] != b2[i]:
erreurs_count += 1
return erreurs_countQuestion 5.
def degre(b):
for i in range(len(b)):
if b[i] == 1:
return len(b) - 1 - i
return -1 # Pour le cas du polynôme nulQuestion 6.
def plus(b, C):
resultat = []
for i in range(len(b)):
if b[i] == C[i]:
resultat.append(0)
else:
resultat.append(1)
return resultat
Question 7.
def degre(b):
for i in range(len(b)):
if b[i] == 1:
return len(b) - 1 - i
return -1
def plus(b, g):
resultat = []
for i in range(len(b)):
if b[i] == g[i]:
resultat.append(0)
else:
resultat.append(1)
return resultat
def CRC(b, g):
n = len(b)
k = len(g) - 1
b = b + [0] * k # Ajout de k zéros à la fin
while degre(b) >= k:
# Aligner et soustraire le polynôme g
for i in range(k + 1):
b[degre(b) - k + i] = ou_exclusif(b[degre(b) - k + i], g[i])
return b[-k:]


