Ce cours me semblait le plus difficile pour moi quand j’étais en Prépas, mais maintenant Je n’arrive pas à croire que c’est aussi simple.
Le problème est que beaucoup de profs n’expliquent pas les choses de manière simple, et ne donne pas l’utilité de ces notions dans la vie réelle ce qui ne permet pas d’imaginer bien les choses.
Mais reste tranquille parce qu’on va t’expliquer tout.
On commence : بسم الله
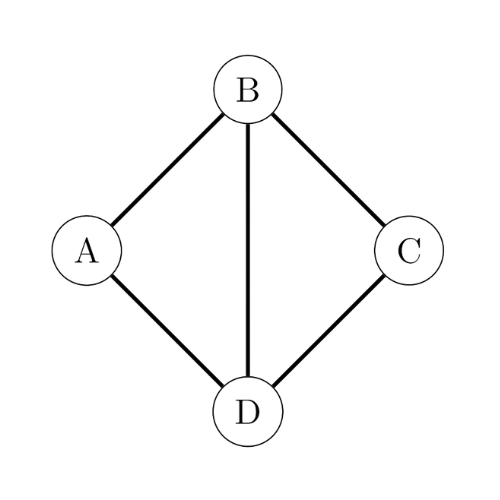
Un graphe est simplement une manière de représenter visuellement des relations ou des connexions entre différents éléments. Il permet de mieux comprendre comment ces éléments sont liés.
L’utilisation des graphes dépend du problème que l’on cherche à résoudre. Dans ce cours, nous allons voir les bases de la théorie des graphes et apprendre à utiliser quelques algorithmes qui sont très utiles pour les ingénieurs.
Pour donner un exemple concret, imaginons que l’on souhaite relier des villes entre elles par des autoroutes. Si on relie chaque ville à toutes les autres, cela coûterait une fortune. La question est donc de savoir comment relier toutes les villes en utilisant le moins de routes possible, tout en gardant les coûts bas.
En modélisant les villes comme des « sommets » dans un graphe, et les autoroutes comme des « arêtes » (lignes reliant les sommets), on peut appliquer des algorithmes de graphes pour trouver la meilleure solution à ce problème.
Graphe orienté, Graphe pondéré
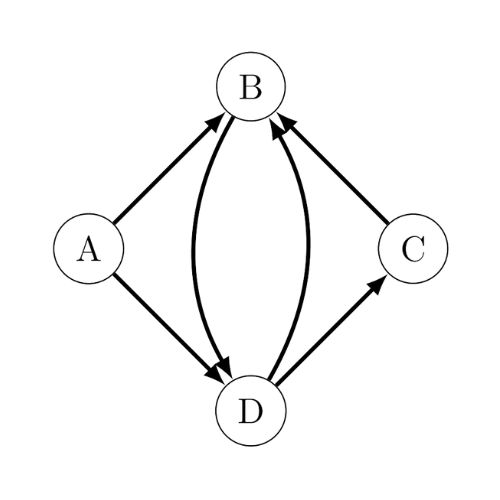
- Graphe orienté: C’est un graphe où les relations représentées par des arêtes ont une direction, ce qui signifie qu’elles ne sont pas nécessairement réciproques. Par exemple, imaginons une voie piétonne et une route pour véhicules. La voie piétonne a une relation réciproque : si un piéton peut aller d’un point A à un point B, il peut aussi revenir de B à A en suivant le même chemin. En revanche, sur une route de conduite, une voie allant de A à B ne garantit pas qu’il existe une voie pour revenir de B à A. Dans ce cas, la relation est unidirectionnelle, ce qui correspond à la définition d’un graphe orienté.
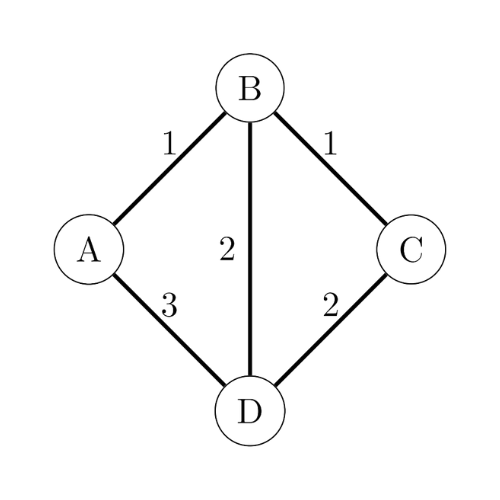
- Graphe pondéré: C’est un graphe dans lequel les relations entre les éléments (représentées par des arêtes) ont des valeurs différentes, ou « poids ». Cela signifie que chaque relation entre deux éléments peut avoir une importance ou une intensité différente. Par exemple, si l’on modélise le réseau routier du Maroc en représentant les villes par des sommets et les routes par des arêtes, la route entre Casablanca et Tanger n’est pas équivalente à celle entre Tanger et Tétouan. Bien qu’il s’agisse dans les deux cas d’une route entre deux villes, elles diffèrent par leur longueur : le trajet Casablanca-Tanger mesure 343 km, tandis que celui de Tanger-Tétouan est de seulement 62 km, donc aller de Casablanca à Tanger doit etre représenté différemment qu’un voyage de Tétouan à Tanger. Ce poids (ici, la distance) attribué à chaque arête différencie un graphe pondéré d’un graphe non pondéré.
Chemin
Soit G un graphe (orienté ou non orienté) et soit s et b deux sommets. Un chemin de s vers b est de la forme s -> i1 -> i2 -> . . . -> ir -> b où les ik sont des sommets intermédiaires et tels qu’il existe un arc de s vers i1, une arc de i1 vers i2 etc. et de ir vers b. Dans le cas où s = b (retour au même point de départ) et qu’il y a au moins une arête/arc, on dit que le chemin est un cycle.

- (D, C, B) est un chemin de D vers B
- (B, C, D) est un chemin de B vers D
- (A, B, D, A) est un cycle
- (B, D, B) est un cycle
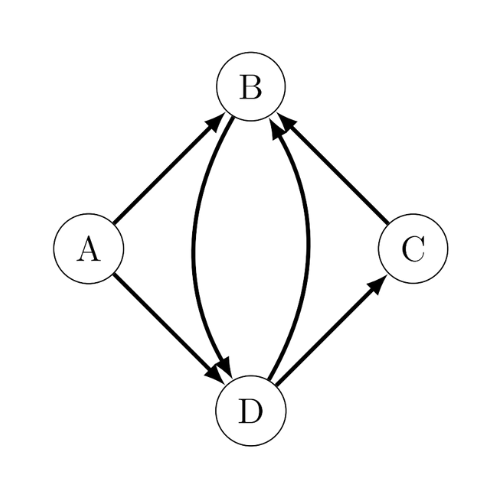
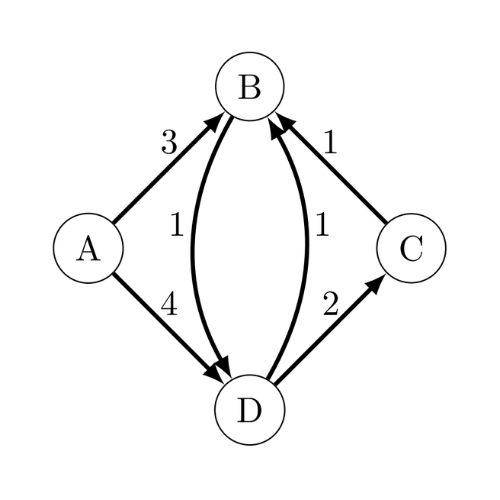
- (D, C, B) est un chemin de D vers B
- (B, C, D) n’exsite pas, c’est non défini car il l’arc (B,C) n’existe pas.
- (A, B, D, A) n’est un cycle
- (B, D, B) est un cycle
Regarde BIEN les différences pour bien comprendre, et bien sur tu peux prendre un rendez vous avec nous
Voisins et degré d’un sommet
- Si G est un graphe non orienté et s un sommet, alors on définit le degré de s comme le nombre de sommets v tel qu’il existe une arête reliant s à v, on note d(s) ce degré. On dit que v est un voisin de s.
- Si G est un graphe orienté et s un sommet, on définit le degré extérieur de s comme le nombre de sommets v tel qu’il existe un arc qui va de s à v, on note d+(s) ce degré. On définit le degré intérieur de s comme le nombre de sommets v tel qu’il existe un arc qui va de v à s, on note d–(s) ce degré.

- Les voisins de B sont A, C et D : d(B) = 3
- Les voisins de A sont B et D : d(A) = 2

- La notion de « voisin » n’est pas définie pour les graphes orientés
- d+(B) = 1 et d–(B) = 3
- d+(A) = 2 et d–(A) = 0
| Graphe orienté | Graphe non orienté |
|---|---|
| arc (s, s’) : couple, l’ordre est important | arête {s, s’} : ensemble – l’ordre n’intervient pas |
| – s’ successeur de s lorsque (s, s’) est un arc – s’ prédécesseur de s lorsque (s’, s) est un arc | s’ adjacent à s lorsque {s, s’} est une arête |
| – d+(s) : degré sortant de s = nombre d’arcs (s, s’) – d-(s) : degré entrant de s = nombre d’arcs (s’, s) – d(s) = d+(s) + d–(s) : degré du sommet | d(s) : degré de s = nombre d’arêtes contenant le sommet s |
| chemin (a1, …, ap) : p-uplet d’arcs tels que l’extrémité terminale de ai et l’extrémité initiale de ai+1 | cycle : chaîne dont les arêtes extrêmes ont un sommet en commun |
| circuit : chemin tel que l’extrémité initiale du premier arc est l’extrémité terminale du dernier arc | chaîne (a1, …, ap) : p-uplet d’arêtes tels que les arêtes ai et ai+1 aient une extrémité commune |
Codage d’un graphe
Pourquoi est-il important de savoir comment coder un graphe ? Après tout, il s’agit simplement d’un dessin avec quelques sommets, non ?
Eh bien, ce n’est pas si simple.
En fait, il ne suffit pas de l’analyser visuellement. Les classes préparatoires te forment pour devenir ingénieur, et un ingénieur doit être capable de modéliser, analyser, et optimiser des problèmes complexes.
Souvent, cela implique de travailler avec des graphes qui peuvent contenir des milliers de sommets et des millions d’arêtes (si on modélise par exemple les transactions entre les gens dans le monde, ou bien les chemins routiers dans tout un pays)
Dans de tels cas, l’analyse manuelle est impossible.
Il devient donc indispensable de savoir coder ces graphes (ou au moins le principe de codage) afin de les traiter avec des algorithmes performants et de tirer parti de la puissance des machines pour gérer et résoudre ces problèmes.
Il existe deux façons de coder un graphe : par une matrice ou par un dictionnaire.
Matrice d’adjacence
On numérote les sommets de 0 à n – 1. On définit la matrice d’adjacence A avec aij = 1 lorsqu’il y a un arc/une arête entre les sommets i et j.
- La matrice est symétrique si le graphe est non orienté,
- À la place de mettre 1, on peut placer le poids de l’arc/arête pour un graphe pondéré
Exemples : en numérotant les sommets de 0 à 4 au lieu de A à E :
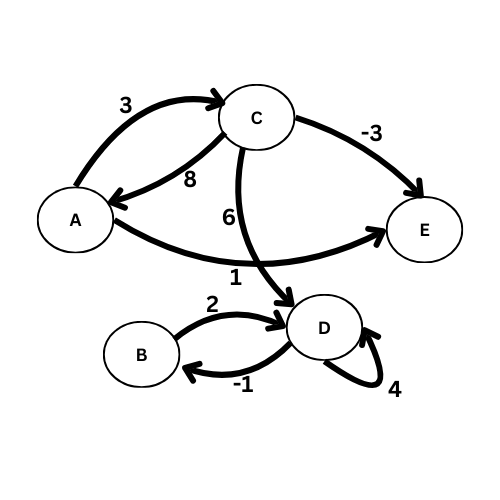

$$ A_2 = \begin{pmatrix} 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 8 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix} $$
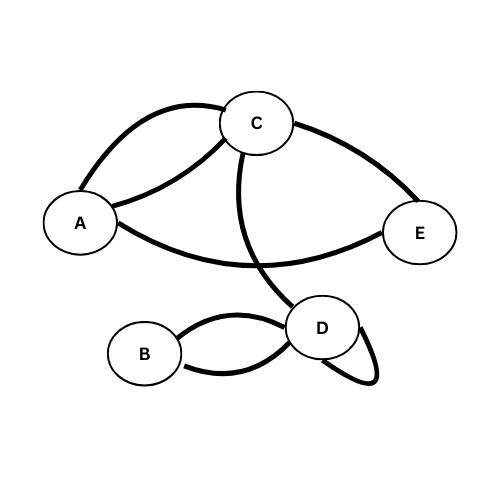
$$ A_3 = \begin{pmatrix} 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 \\ \end{pmatrix} $$
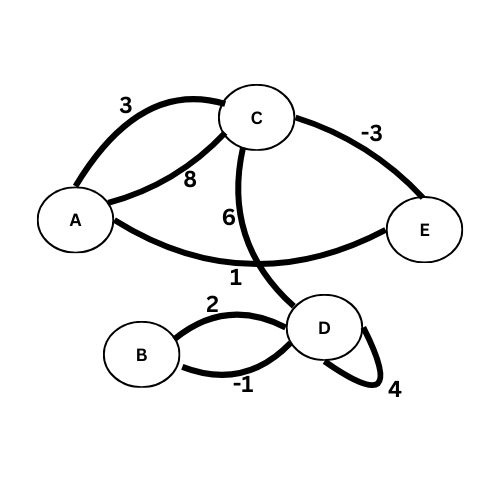
$$ A_4 = \begin{pmatrix} 0 & 0 & 3 & 0 & 8 \\ 0 & 0 & 0 & 2 & 0 \\ 3 & 0 & 0 & 6 & -3 \\ 0 & 2 & 6 & 0 & 1 \\ 8 & 0 & -3 & 1 & 0 \\ \end{pmatrix} $$
Avantages :
- On sait facilement s’il y a un arc/une arête entre 2 sommets,
- On gère facilement les poids,
- On peut obtenir les sommets initiaux/terminaux en regardant sur la ligne/colonne correspondante
Inconvénients :
Déterminer les sommets adjacents d’un sommet nécessite de parcourir toute une ligne/colonne (complexité en O(n))
II.2 Liste d’adjacence
Pour chaque sommet s, on donne sa liste de sommets adjacents s’ (de sorte que (s, s’) est un arc ou {s, s’} une arête). Cela peut également être réalisé à l’aide d’un dictionnaire, ce qui permet de conserver les noms des sommets.
On peut gérer les poids en associant à un sommet les couples sommet adjacent/poids ou un nouveau dictionnaire avec les sommets en clé et les poids en valeur,
Exemples :

Arc = {
‘A’: [(‘C’, 3), (‘E’, 8)],
‘B’: [(‘D’, 1)],
‘C’: [(‘A’, 8), (‘D’, 6), (‘E’, -3)],
‘D’: [(‘B’, -1), (‘E’, 4)],
‘E’: []
}

Arc = {
‘A’: [‘C’, ‘E’],
‘B’: [‘D’],
‘C’: [‘A’, ‘D’, ‘E’],
‘D’: [‘B’, ‘E’],
‘E’: []
}

Arc = {
‘A’: [‘C’, ‘E’],
‘B’: [‘D’],
‘C’: [‘A’, ‘D’, ‘E’],
‘D’: [‘A’, ‘B’, ‘E’],
‘E’: [‘A’, ‘C’]
}

Arc = {
‘A’: [(‘C’, 3), (‘E’, 8)],
‘B’: [(‘D’, 1)],
‘C’: [(‘A’, 8), (‘D’, 6), (‘E’, -3)],
‘D’: [(‘B’, -1), (‘E’, 4)],
‘E’: [(‘A’, 8), (‘C’, -3)]
}
Avantages :
- on a directement la liste des sommets successeurs (utile par exemple pour tous les algorithmes de parcours),
- il est plus ou moins facile de savoir si un arc/une arête existe
Inconvénients :
Algorithmes de Parcours:
L’un des utilités d’un parcours est qu’il permet de détecter la présence de cycles et permet de savoir si un graphe non orienté est connexe.
Pour savoir si un graphe est connexe, il suffit de faire un parcours et de vérifier si tous les sommets du graphe ont été visités. Il suffit donc de comparer la longueur de la liste des éléments visités V à l’ordre du graphe.
NB: Le parcours est appliqué sur n’importe quel type de graphe, on va boir les exemples pour les graphes orientés pour bien comprendre le fonctionnement des algorithmes; les graphes non orientés peut etre transformés en graphes orientés tel que chaque arête va etre transformé en 2 arcs de sens inverses.
C’est quoi un graphe connexe??
Soit G un graphe non orienté, on dit qu’il est connexe si pour tous sommets s et b il existe au moins un chemin de s à b.
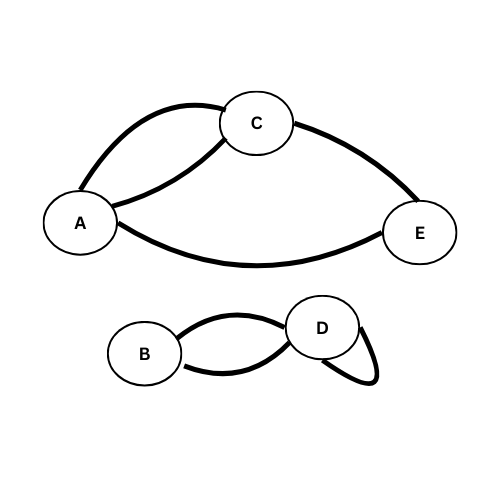
Non connexe (n’existe aucun chemin de A à B)

Graphe Connexe
Parcours en Largeur
Principe
On choisit un sommet, on stocke tous ses voisins (niveau 1).
Puis on regarde les nouveaux voisins (niveau 2) de chacun de ces premiers voisins et ainsi de suite jusqu’à ne plus avoir de voisins.
On peut à mesure stocker différentes informations : les successeurs d’un sommet, son prédécesseur (un sommet n’en a qu’un seul).
On remarque ainsi que cela permet de calcul la distance la plus courte entre le point de départ et les sommets du graphe (on peut même retrouver le chemin en partant de la fin et en remontant dans la liste des prédécesseurs) .
Évidemment le parcours va dépendre de l’ordre des successeurs d’un sommet (notamment pour l’arbre de parcours obtenu)
Code
Un exemple de programme dans lequel on détermine, par un parcours en largeur, les distances au sommet d’origine, les successeurs d’un sommet dans ce parcours et le prédécesseur (unique) de chacun des sommets. Ce programme fonctionneaussi bien sur un graphe orienté que sur un graphe non orienté
Fonctionnement étape par étape:
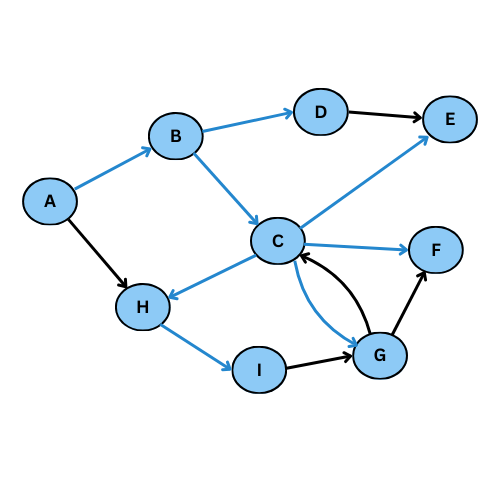
On va executer l’algorithme manuellement sur le graphe suivant:
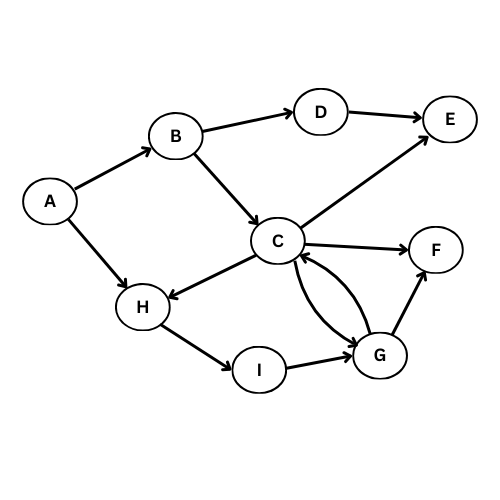
NB: On va suivre l’ordre alphabétique s’il y a plus qu’un voisin
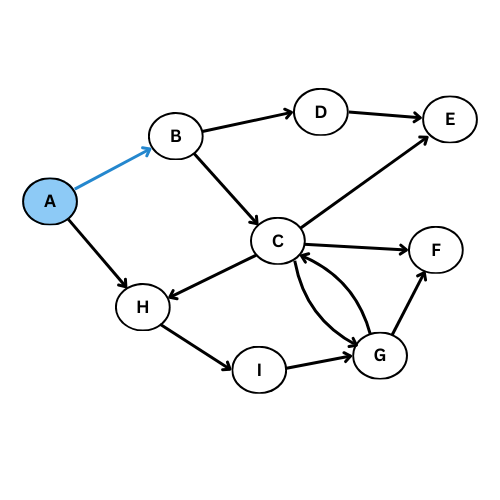
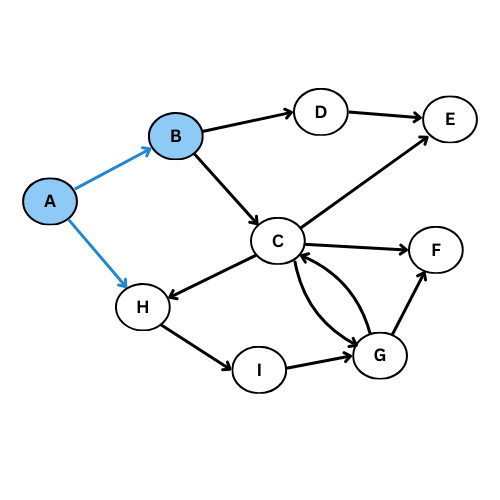
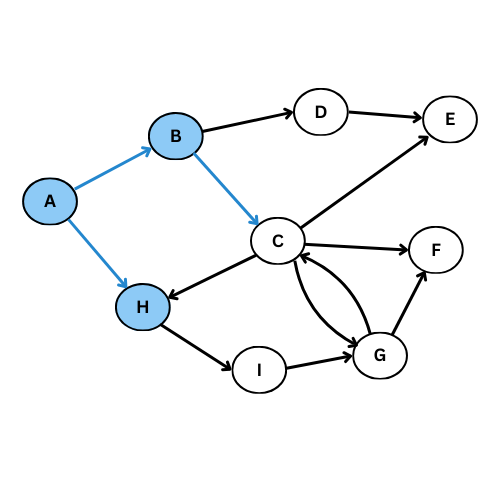
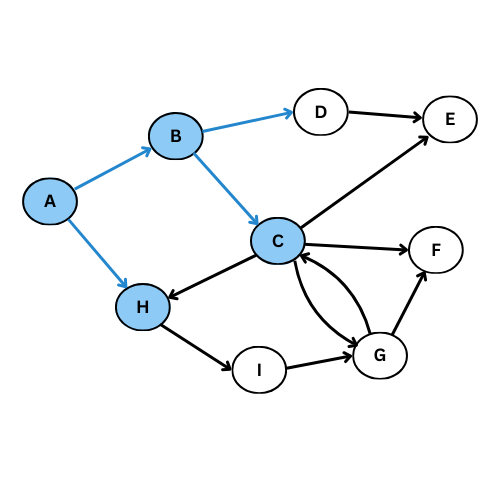
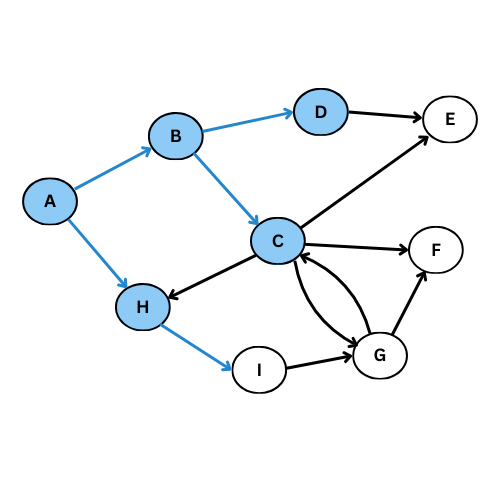
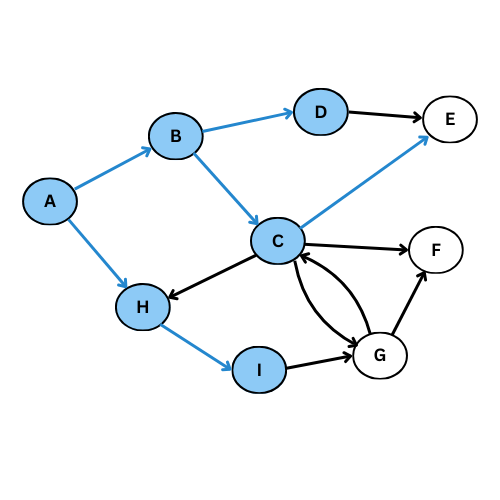
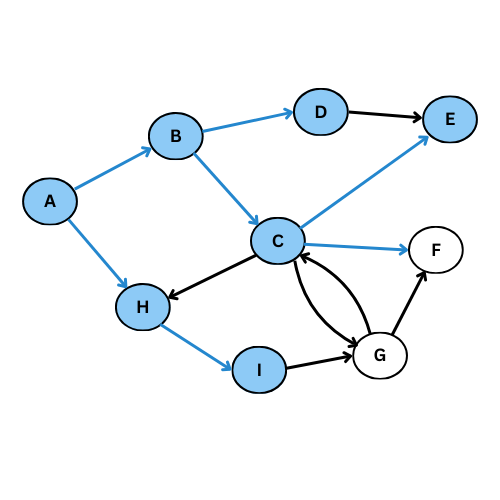
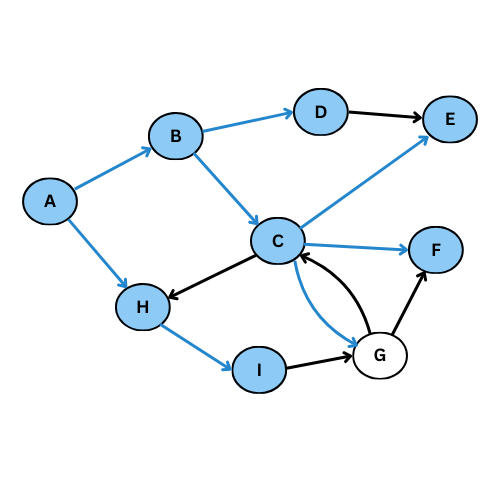
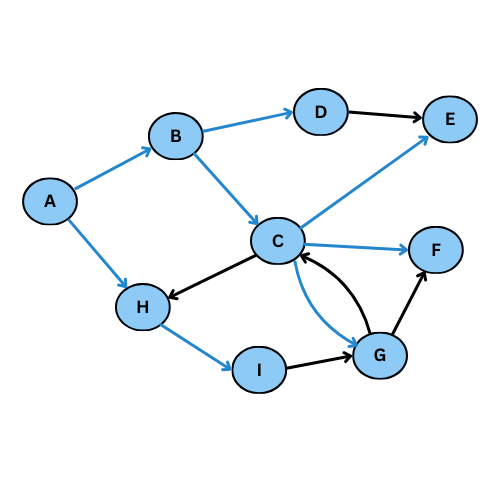
Comme tu vois, plusieurs arcs ne sont pas considéré, on obtient ce graphe de parcours:
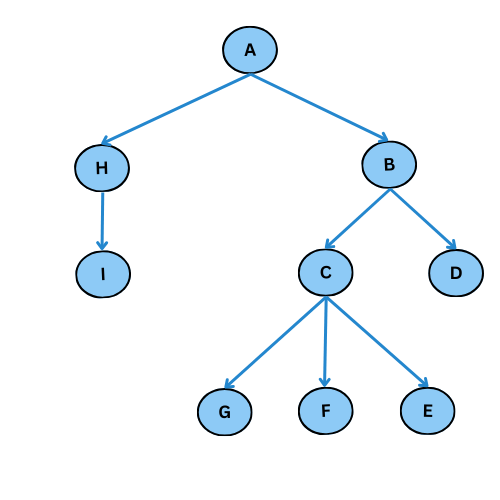
Pour mieux comprendre, donne le code du graphe initiale, execute la fonction parcours_largeur , regarde l’output et compare avec le graphe de parcours dessiné
On peut recréer facilement le chemin parcouru à partir du dictionnaire des prédécesseurs :
Si on note P1 le dictionnaire des prédécesseurs donné par la fonction parcours_largeur, on doit obtenir ‘ABCF’ si on exécute parcours(‘F’, P1)
!! Remarque: Utilisation d’une file
On a ici utilisé une liste sur laquelle on retire le premier élément (P.pop(0)).
La complexité de cette opération est en O(n) si n est la taille de la liste.
On ajoute également des éléments en fin de liste.
La structure intéressante pour réaliser cette opération est celle de file (en utilisant par exemple les deque du modules collections: from collections import deque).
Parcours en Largeur
Principe
Le parcours se fait différemment cette fois : en partant d’un sommet, on essaie d’aller le plus loin possible dans le graphe, avant de revenir sur nos pas pour poursuivre l’exploration. Contrairement au parcours en largeur où la bonne structure pour les sommets est une file (le premier sommet stocké sera le nouveau point de départ), on utilise cette fois une pile qui va décrire le parcours actuellement réalisé (le bas de la pile est le sommet de départ, le haut le sommet en cours). On fera également attention de ne pas boucler (c’est-à-dire de ne pas repasser par un sommet déjà exploré ou en cours d’exploration).
Code
Fonctionnement étape par étape:
On reprend le meme exemple précédent pour voir la différence:

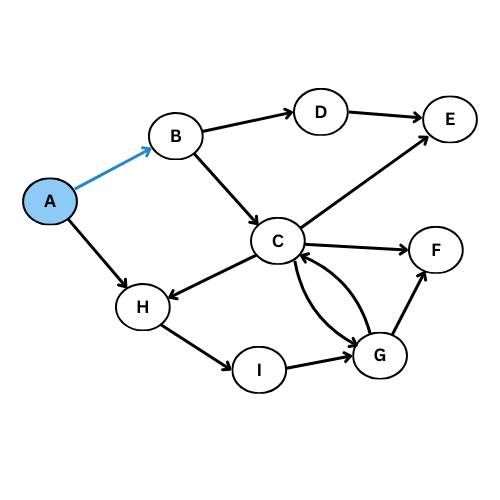
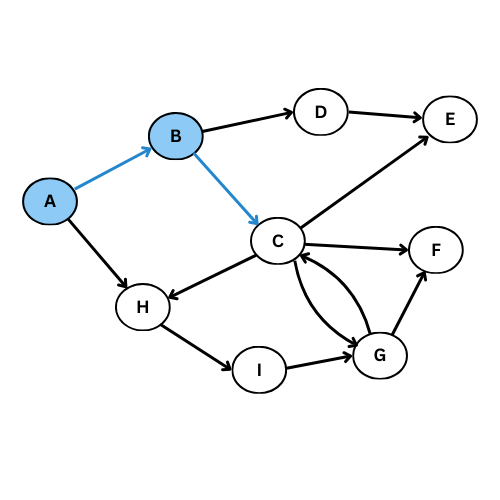
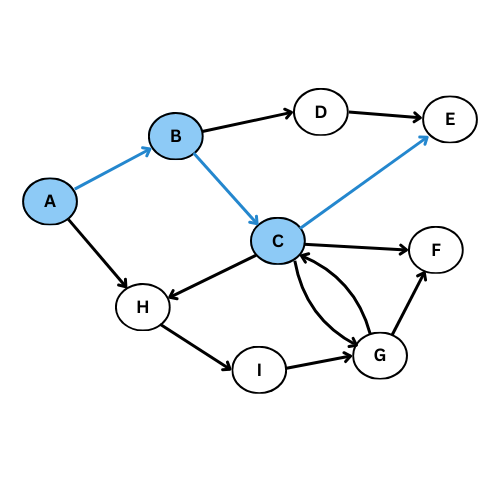
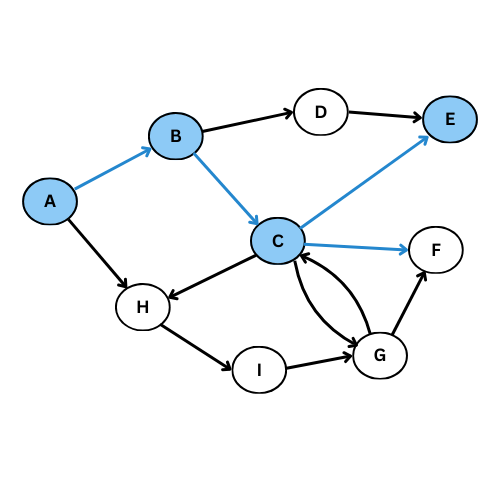
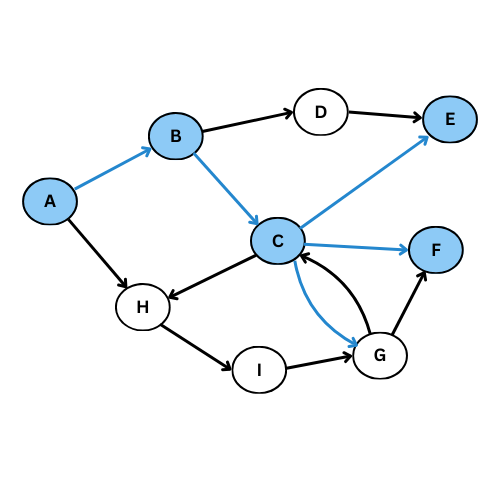
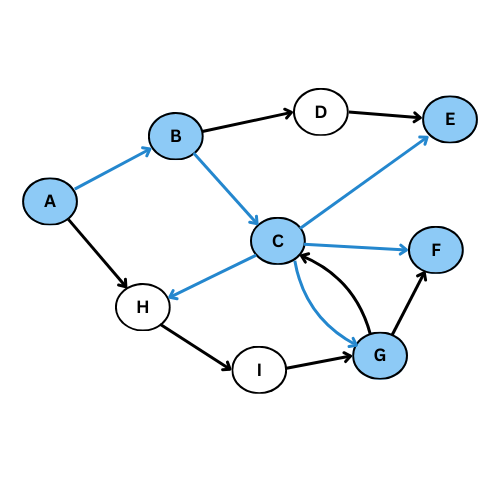
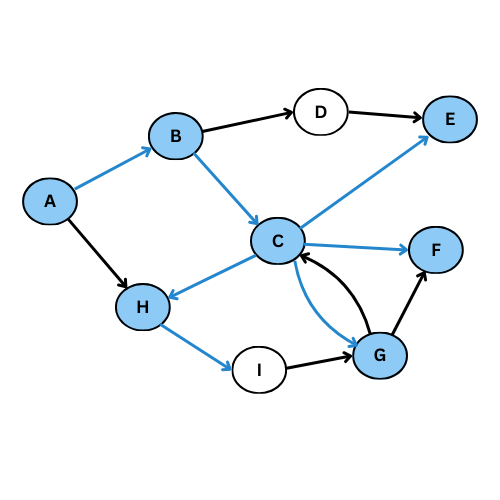
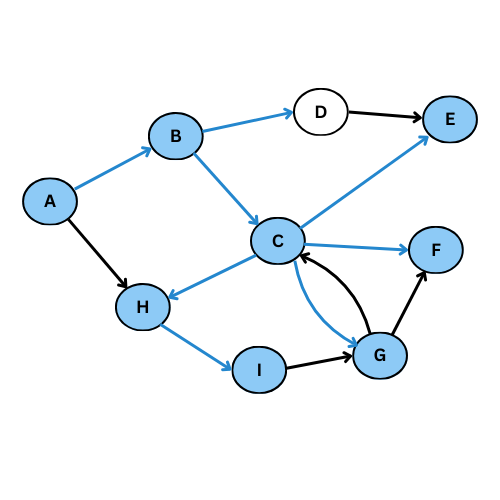
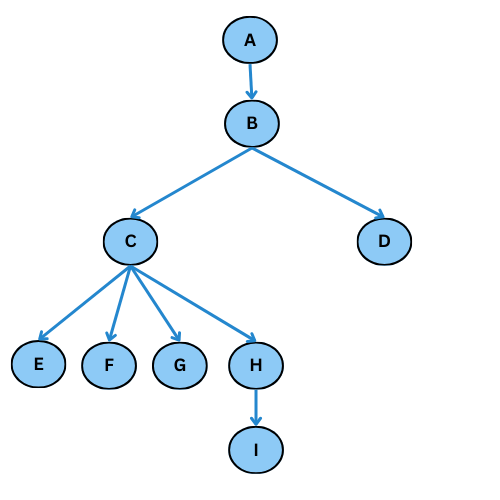
Le graphe de parcours est dans ce cas:
Remarque Importante
L’algorithme de parcours en profondeur permet, pour des graphes non orientés (c’est ce qui est MARQUE au Programme), de détecter certains cycles. Si on reprend l’exemple du paragraphe précédent, on va créer une chaîne passant par les sommets A, B, C, E, D. On se rend compte que D n’a pas de voisin non marqué mais a un voisin marqué dans le chemin (les éléments de statut 1 dans le programme précédent), à savoir B. On en déduit l’existence d’un cycle BCDEB. Évidemment on ne détectera pas tous les cycles par ce moyen.
Amélioration de compléxité
- ‚ À chaque fois, on vérifie si les éléments sont dans la liste des sommets déjà visités. Or, vérifier si un élément est dans une liste de longueur n a une complexité de O(n). À la place, on peut mettre en place un dictionnaire, et on ajoute les sommets comme clés du dictionnaire à chaque fois qu’on les visite. Seulement, pour des raisons qui seront expliquées l’année prochaine, vérifier si un élément une clé d’un dictionnaire ayant n clés n’est pas en O(n) mais en O(1). Ce qui signifie que le temps de cette vérification est le même quelque soit le nombre de clés dans le dictionnaire.
- ‚ Dans une file, on retire le premier élément de la liste avec un .pop(0) qui a une complexité en O(n) : Tandis que .pop(), enlève le dernier élément de la liste, se fait en O(1). Pour cette raison, peut modéliser les files non pas avec des listes mais avec une structure similaire appelée deque (
from collections import deque).


