Les Matrices en Python - Al Mouhandis

Pour pouvoir travailler avec les matrices en Python, on a choisit des les représenter par la liste des lignes et chaque ligne est une liste des éléments.
Donc c’est une liste de listes.

Exemple:

La matrice :
$$ \begin{pmatrix} 0 & 0 & 3 & 0 & 1 \\ 0 & 0 & 2 & 0 & 0 \\ 8 & 0 & 0 & 6 & -3 \\ 0 & -1 & 0 & 4 & 0 \end{pmatrix} $$

est représentée par :
[[0, 0, 3, 0, 1],
[0, 0, 2, 0, 0],
[8, 0, 0, 6, -3],
[0,-1, 0, 4, 0]]

Accéder à une case d’une matrice

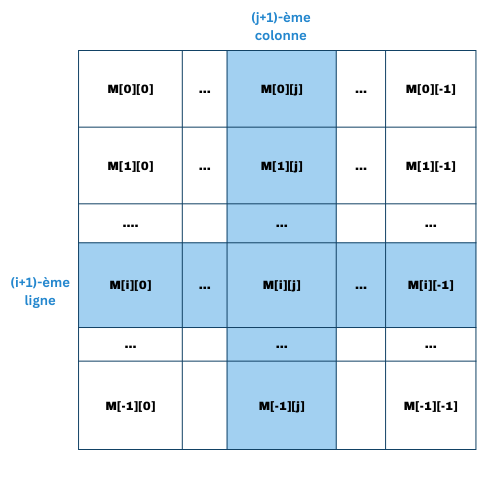
Considérons une matrice M de n lignes et p colonnes. Pour accéder à l’élément situé à la (i+1)-ème ligne et (j+1)-ème colonne (avec 0 <= i <= n-1 et 0 <= j <= p-1), quelle instruction devons-nous exécuter ?

Rappel : Accès aux éléments d’une liste

Dans une liste L, pour accéder à l’élément situé à la (j+1)-ème position, on utilise l’instruction L[j]. De même, puisque chaque ligne de la matrice M est une liste, l’accès à un élément particulier se fait en deux étapes :

On sélectionne la (i+1)-ème ligne, soit M[i].
On sélectionne ensuite le (j+1)-ème élément de cette ligne, soit M[i][j].

Ainsi, pour accéder à l’élément de la (i+1)-ème ligne et (j+1)-ème colonne de la matrice M, l’instruction à exécuter est : M[i][j].

Essaye des syntaxes ici pour t’adapter bien à la logique des matrice:

Création d’une matrice

Si on veut créer une matrice M (de n lignes et p colonnes) en suivant certain modèle/formule, vaut mieux utiliser la boucle for, il y’a 2 manières pour le faire:

Syntaxe détaillé:
1. On définit M comme une liste vide
2. On exécute une boucle for allant de 0 à n-1 pour créer les lignes
  1. On définit la i-ème ligne comme liste vide
  2. On exécute une boucle for allant de 0 à p-1 pour créer les colonnes de la i-ème ligne
    1. On ajoute M[i][j] (qui suit un certain pattern) à la liste (i-ème ligne)
  3. Quand la 2ème boucle est terminée (la ligne i contient p cases), on ajoute la ligne à M
3. Quand la 1ère boucle est terminée, M est construite
Syntaxe concise:
1. Dans une seule ligne de code on exécute M = [ [M[i][j] for j in range (p)] for i in range(n) ]
  (Fait ATTENTION à l’ordre des boucles où la notation de i et j, il est meiux de toujours utiliser i pour les lignes et j pour les colonnes)

Exemple 1

Ecrire une fonction qui prend 2 arguments n et p et crée une matrice de n lignes et p colonnes et toutes les cases vaut 0

Dans ce cas: M[i][j] = 0 pour tout i et j

Syntaxe détaillé

Syntaxe concise

Exemple 2

Ecrire une fonction qui prend 2 arguments n et p et crée une matrice d’entiers de n lignes et p colonnes, la 1ère ligne vaut : 1, 2, 3, ... et la 1ère case de chaque ligne est égale à la dernière case de la ligne précédente augmentée de 1.
Pour n=2 et p=3: M = [[1, 2, 3], [4,5,6]]

Dans ce cas : M[i][j] = i*p + j+1

Syntaxe détaillé (sans savoir la formule exacte)

Syntaxe concise

Exemple 3

Ecrire une fonction qui prend un seul argument n et crée la matrice identité I

Dans ce cas : M[i][j] = 1 si i=j et 0 sinon

Syntaxe détaillé (sans savoir la formule exacte)

Syntaxe concise

Syntaxe concise (pour les Développeurs du futur)